[ad_1]
Warren Buffett at the time challenged Invoice Gates to an unusual recreation of dice. Buffett positioned 4 dice on the desk and explained the procedures. They would each choose a die, roll it a bunch of times, and whoever rolled a better number a lot more often would acquire. These weren’t numbered like normal dice. The common one as a result of six have been changed with other figures that varied from die to die. As a supposed courtesy, Buffett invited Gates to pick his die 1st. This aroused suspicion, compelling Gates to examine the dice for himself and then insist that Buffett pick initially.
Usually, deciding upon first in game titles confers an benefit, so why had been these moguls dueling for second choose? The response lies in a peculiar home of Buffett’s dice. To enjoy it, let us inspect an case in point of related dice that have the very same residence as those people utilised by Buffett but that are easier to evaluate.


How often will die A roll better than die B? Mainly because there are just three distinct numbers on each die, one particular third of the time, die A will roll a 9, which wins irrespective of B’s roll. Just one 3rd of the time, A will roll a 1, which loses irrespective of B’s roll. And the remaining third of the time, A will roll a 5, which wins on two thirds of B’s rolls (the kinds that change up 3 or 4). Aggregating these observations with the regulations of probability, we get that A beats B (⅓ x 1) + (⅓ x ) + (⅓ x ⅔) = 5/9, or about 56 per cent of the time. A related calculation yields an similar acquire share for B over C. That is, B also beats C about 56 p.c of the time. So if A commonly beats B and B normally beats C, then undoubtedly A must typically beat C, right? Completely wrong! C in fact beats A about 56 p.c of the time as very well.
We phone these delinquent cubes intransitive dice. Several relations encountered in everyday living exhibit the opposite, transitive house: If Alicia is more mature than Bruno and Bruno is more mature than Cassandra, then Alicia is more mature than Cassandra. That is a valid deduction since the relation “is older than” obeys the transitive home. Intransitive dice shock our intuitions since the relation “typically rolls bigger than” is not transitive, even nevertheless it appears like it should really be. Take note that to roll greater than die B on average, die A doesn’t want to generally roll better. And critically, there is overlap among instances in which A beats B and A loses to C. This interleaving of the quantities on the faces enables the intransitivity.
With any established of intransitive dice, whoever chooses very first in Buffett’s video game bears a disadvantage, mainly because the next participant can generally decide on the die that is likely to defeat their opponent’s alternative. Several men and women very first come across intransitive online games by means of rock paper scissors. Its cyclic winning structure ensures that no decision uniquely outranks any other. Buffett’s dice match is akin to tricking your opponent into asserting what they intend to toss up coming in rock paper scissors—a mistake that would expense them the recreation.
Stanford statistician Bradley Efron invented intransitive dice more than 50 years ago. Each individual die in Efron’s established of four beats a different an remarkable two thirds (about 67 percent) of the time. Martin Gardner popularized Efron’s dice in his legendary “Mathematical Games” column at Scientific American, but mathheads have devised numerous clever variants since then. We now know that any selection of dice (higher than two) can exhibit an intransitive cycle, this means, for instance, there exists a set of 26 dice in which die A usually beats die B, which ordinarily beats C, which usually beats D, and so on all the way via to die Z, which, in spite of residing at the stop of a lengthy chain of dominating dice, pulls an upset by cycling back and typically beating A.
Intransitive dice have to have not include six sides. In reality, intransitive trios of dice with any quantity of sides (greater than two) exist. Dutch puzzle maker Oskar van Deventer even invented a established of 7 6-sided dice that permit for 3 players in Buffett’s sport. In other phrases, if Buffett and Gates invited Dolly Parton to play dice with them, then Gates and Parton could each choose their pick from the 7, and Buffett would nevertheless constantly have a die in the remaining five that typically beats both of their possibilities.
Just when you imagine you have wrapped your head all-around the peculiar behavior of intransitive dice, the good development below will roll you correct again to dumbstruck awe.
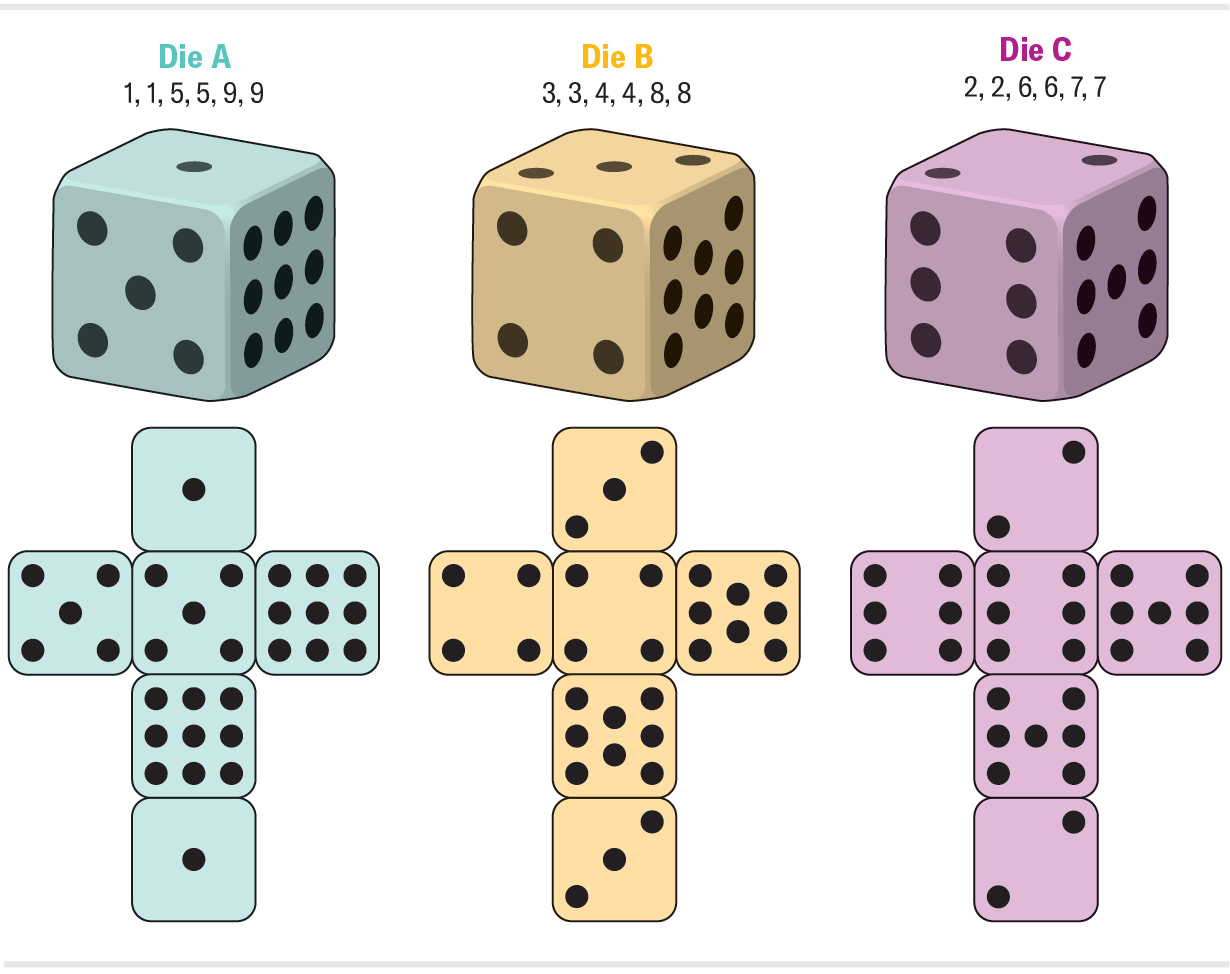
![Graphic shows the following three die “unwrapped”: Die A [3, 3, 3, 3, 3, 6], Die B [2, 2, 2, 5, 5, 5], Die C [1, 4, 4, 4, 4, 4], and shows that in a comparison of which die rolls a higher number more often, A beats B, B beats C, and C beats A.](https://static.scientificamerican.com/sciam/assets/Image/2023/intransitiveDice_graphic_20230915_d2.png)


1 can compute that A beats B 7/12 (about 58 %) of the time B beats C 7/12 of the time and C beats A 25/36 (about 69 per cent) of the time. So much, very little we haven’t observed right before. These do not conquer every single other with similar possibilities, but they’re even now intransitive. Typically dice arrive in pairs. When you think about rolling dice, you in all probability photograph two identical dice in your hand and summing the numbers that transform up on each and every. What takes place if we roll pairs of dice from the figure higher than? What is the probability that two copies of die A roll a sum that beats two copies of die B? Is it the very same as ahead of given that the copies are identical, or does duplicating the dice amplify the benefit that A has more than B? In a stunning twist, the influence reverses. The pair of A dice typically lose to the pair of B dice! What’s far more, the full cycle reverses: a pair of B dice ordinarily eliminate to a pair of C dice and a pair of C dice ordinarily lose to a pair of A dice. Procuring a set of these dice is a trusted way to get banned from spouse and children match evening.
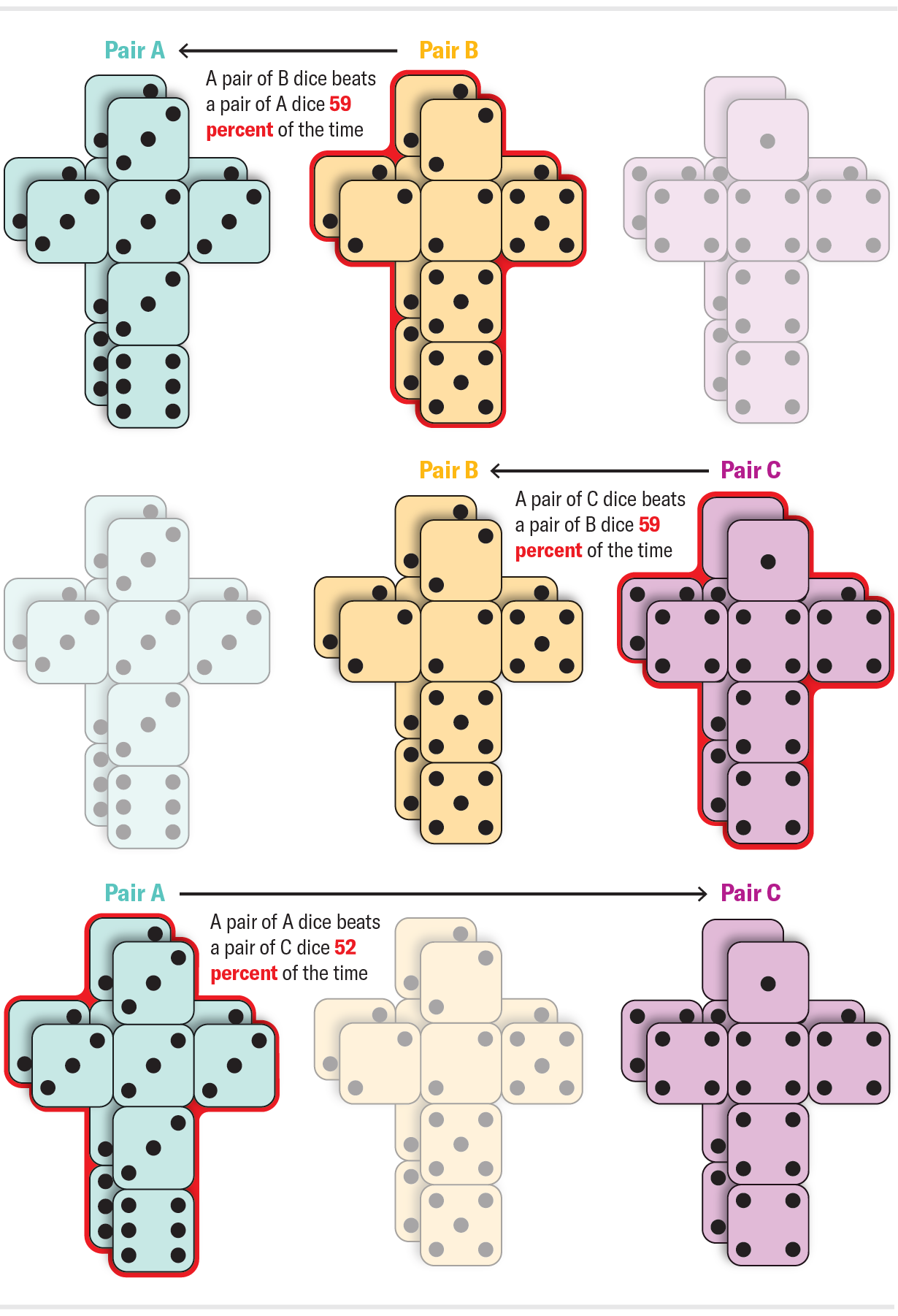


To get a come to feel for how duplicating dice could reverse their relative power, consider the very simple circumstance of two two-sided dice, X and Y. Equally of X’s faces have a 1 on them, even though Y’s faces are and 3. These dice have equal toughness. Y wins 50 percent of the time (when it rolls a 3) and loses half of the time (when it rolls a ). When we duplicate the dice on the other hand, the Y pair becomes more powerful than the X pair. The X pair always rolls a total of 2. The Y pair only loses if both of those of them switch up , which only transpires one particular quarter of the time. A very similar phenomenon points out the reversal in the determine over.
It is not obvious that intransitive dice ought to exist at all. But is that because they are exceptional? If all you know about a trio of dice is that A usually beats B, and B typically beats C, is it far more most likely that A normally beats C or vice versa? Clever people today have meticulously constructed by hand all of the dice reviewed earlier mentioned, but could they have just picked dice numberings at random and had a respectable shot at getting an intransitive established?
British mathematician Timothy Gowers set out to remedy this concern. Gowers qualified prospects the Polymath Project, an modern and relatively new paradigm for mathematical investigation. As an alternative of a couple mathematicians at a single or two universities chipping away at a problem—the usual study model in math —the Polymath Task will take a crowdsourcing solution. Any variety of contributors can collaborate on a proof by means of online forum discussion. Gowers considered the intransitive dice concern ripe for a group hard work and proposed it on his blog site in 2017. Replacing a chalkboard with a WordPress responses part, dozens of minds swarmed the challenge and cracked it.
If you randomly assign quantities to a few different dice and then want to know the probabilities that they exhibit intransitivity, it could depend on what just you indicate by “randomly assign numbers” to the dice. The polymath workforce modeled this with two natural requirements. Just as a regular 6-sided die only contains digits in between 1 and 6, a random n-sided die will only incorporate digits among 1 and n (even though some may repeat, and some could not arise at all). Also, the quantities on a common six-sided die increase up to 1 + 2 + 3 + 4 + 5 + 6. To maintain the dice balanced (e.g., no die ought to include all types or solely huge digits), the polymath workforce demanded this of n-sided dice: the sum of their sides ought to equal the sum of the quantities from 1 to n.
Do you want to guess whether transitive or intransitive dice are more popular? Polymath Undertaking contributors proved that 3 random n-sided dice will be intransitive about 50 percent of the time. In other terms, figuring out that A usually beats B, and B commonly beats C, provides you virtually no information and facts about no matter if A will normally conquer C or vice versa. I would have guessed that transitive dice have been additional common than intransitive types. I could picture some suspicious audience, fatigued of possessing their expectations subverted, predicting that intransitive dice are additional frequent than transitive ones. But these slippery dice insist on evading prediction. For a few dice, transitive and intransitive dice are similarly typical.
This is an belief and examination write-up, and the sights expressed by the author or authors are not automatically these of Scientific American.
[ad_2]
Source backlink



