[ad_1]
Have faith in but confirm. That expression captures the tension between relying on other people when however wanting to preserve some stage of management above a predicament. Mathematician Adi Shamir must have considered about this obstacle when he formulated what is now regarded as “Shamir’s top secret sharing,” an algorithm named just after him.
To comprehend it, the next puzzle can enable: Suppose an elderly female would like to bequeath the contents of her safe and sound, which is secured with a mixture lock, to her five sons, but she is suspicious of each individual of them. She fears that if she reveals the code to just a person, he will make off with the contents. So she needs to give just about every son a clue such that only the five doing the job collectively can open up the safe. How need to the woman move forward?
The activity may perhaps seem straightforward. For case in point, if the blend lock required a five-digit code, she could give just about every son a quantity so that they could open it jointly. But in that scenario, if a few sons teamed up, they could most likely bypass their two other brothers. A few allies are only two figures shorter of the total code, so they could swiftly check out out the attainable selection mixtures to get to the coveted contents.
The woman is hence hunting for a way to distribute information that can only be made use of if all five do the job together. If two, a few or 4 of the five sons get jointly, the mixed facts information will have to be useless. And that prerequisite can make the undertaking a great deal additional advanced.
But in 1979 this problem did not discourage Shamir. Two many years before he had made the so-termed “RSA algorithm” jointly with Ron Rivest and Leonard Adleman. It was the first uneven encryption algorithm to be commonly adopted, and it is continue to made use of now.
Shamir’s Solution Sharing in Action
To comprehend the Shamir mystery-sharing strategy, it helps to glimpse at a concrete numerical instance. Suppose the woman’s magic formula code is 43953, and, for the sake of simplicity, let’s believe she only has two sons. (We’ll get the job done our way up to the problem with 5 sons later on.)
If the lady had been to entrust 1 son with “439” and the other with “953,” she would have provided the two of them the exact amount of money of data. Now, as defined over, the sons could just about every attempt to guess the lacking two digits. They would only have to consider a greatest of 100 mixtures each individual to open the risk-free.
Shamir therefore required a distinctive answer. It would be most effective if each and every sons gained a piece of information and facts that at very first glance had almost nothing to do with the remedy. But if you put the two pieces of info jointly, you must be equipped to deduce the range combination 43953. And there is an stylish, uncomplicated way to do this with the help of a linear equation.
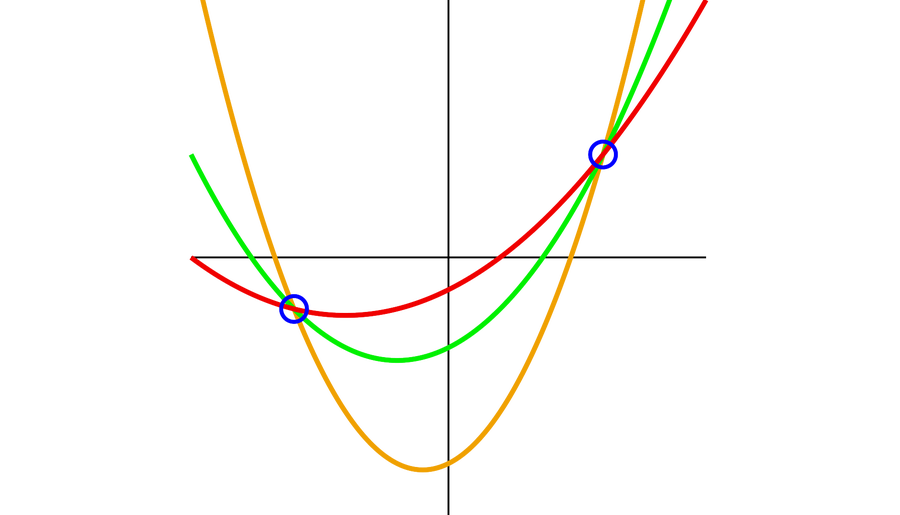
Each individual straight line is uniquely described by two points. Shamir recognized that the key amount can be encoded in a straight line: for illustration, as the height at which it intersects the y axis. If you give the two sons the coordinates of 1 stage each individual on the straight line, they can only identify the amount 43953 collectively. A single of the sons cannot do something with a one issue by yourself: there are an infinite variety of straight lines that run through a one point.
The female could, for instance, decide on the equation of the line y = 5x + 43953 and give the eldest son the coordinates for a position P1 (33503, 211468) and the other son the coordinates for a second place, P2 (85395, 470928). Even if the two sons are lousy at math, they can merely mark the two points in the airplane, connect them with a ruler and then browse off the stage at which the straight line intersects the y axis for the solution to the harmless.
So the difficulty is solved for two sons. If the female has three sons, she could progress in a very similar way. In this circumstance, nevertheless, she would not pick out a straight line but alternatively a parabola to hide the code.
For example, the woman can choose the quadratic function y = 5x2 + 10x + 43953 and give just about every of her sons a level on the parabola. Once again, the issue of intersection with the y axis corresponds to the preferred remedy: 43953. Two of the sons cannot conspire from the 3rd because an infinite variety of parabolas can run by two points the two sons need to have the support of their brother to locate the level of intersection with the y axis and hence the code to the safe and sound.
The basic principle can be generalized for any amount of functions: A woman with four sons can fix an equation of the kind y = ax3 + bx2 + cx + 43953. (For the reason that 3 is the optimum exponent in this equation, it is called a polynomial equation of the 3rd degree.) A woman with five sons utilizes a polynomial equation of the fourth diploma (this kind of as y = ax4 + bx3 + cx2 + dx + 43953), and so on. The theory is based mostly on so-called polynomial interpolation: in general, n + 1 details are demanded to uniquely ascertain a polynomial of the nth degree.
The girl can also give her sons access to the harmless in pairs. In this case she relies on the sons controlling each individual other such that two out of five people have to have to be existing to open the risk-free. To do this, the lady can again decide on a straight line as a foundation and mark five randomly selected details on it. By providing each and every son a stage, she guarantees that two of them can figure out the code—regardless of which two of the sons meet.
But there is a capture. Let’s return to the state of affairs with the five sons. If 4 of them conspire in opposition to a brother, they can use the 4 points to fix the fourth-diploma equation as considerably as probable. Of course, they can’t read through the code right from it. In the conclusion they are left with an equation with two unknowns: a parameter a and the code c (which in our illustration is 43953, but the sons do not know that).
The 4 sons know that c have to be an integer, nonetheless. And if, for illustration, the woman has always offered them integer coordinates for the details on the curve, then they can presume that a in all probability also has an integer benefit. This substantially restricts the range of options. The brothers can use a pc method to try out out various solutions—and might then ascertain the right code.
Into a Different Selection Array
To avoid these a scenario, Shamir experienced yet another trick up his sleeve: alternatively of calculating with the standard serious figures, he restricted himself to a lesser number place: a finite discipline. In this quantity process, the 4 basic arithmetic operations (addition, multiplication, subtraction and division) can be applied as standard. Instead of an infinite range of figures, however, this amount room only includes a finite range of them.
However that could seem unfamiliar, we use finite fields every single day—for illustration, any time we glance at the clock. If you only search at the several hours, the amount vary includes either 12 or 24 quantities. But we still determine in this limited place: if it’s 11 P.M. and anyone claims that the bakery opens in 7 hrs, then it’s apparent that they necessarily mean 6 o’clock.
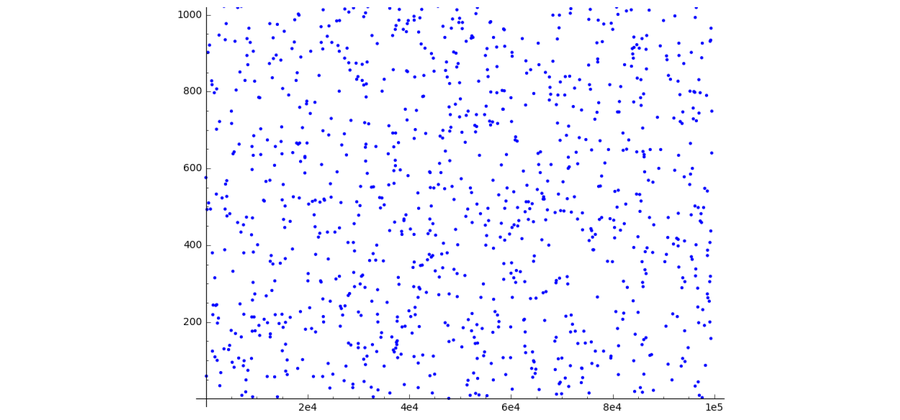
In Shamir’s secret sharing, a restricted variety vary is also picked, but the higher restrict is typically a substantial key amount. If the range room is decided on in this way, the graph of a polynomial no lengthier corresponds to a constant curve but to randomly dispersed details in the plane.
By limiting the woman’s calculations to these a quantity variety, it is virtually impossible for the brothers to conspire versus just about every other. To uncover out the appropriate numerical code, they have to function together.
This post at first appeared in Spektrum der Wissenschaft and was reproduced with authorization.
[ad_2]
Source backlink