[ad_1]
Typically, there are very clear responses in mathematics—especially if the duties are not way too complicated. But when it arrives to the Sleeping Attractiveness challenge, which grew to become popular in 2000, there is nevertheless no universal consensus. Authorities in philosophy and arithmetic break up into two camps and ceaselessly cite—often really convincingly—arguments for their respective aspect. Extra than 100 complex publications exist on this puzzle, and practically each individual man or woman who hears about the Sleeping Elegance assumed experiment develops their possess robust opinion.
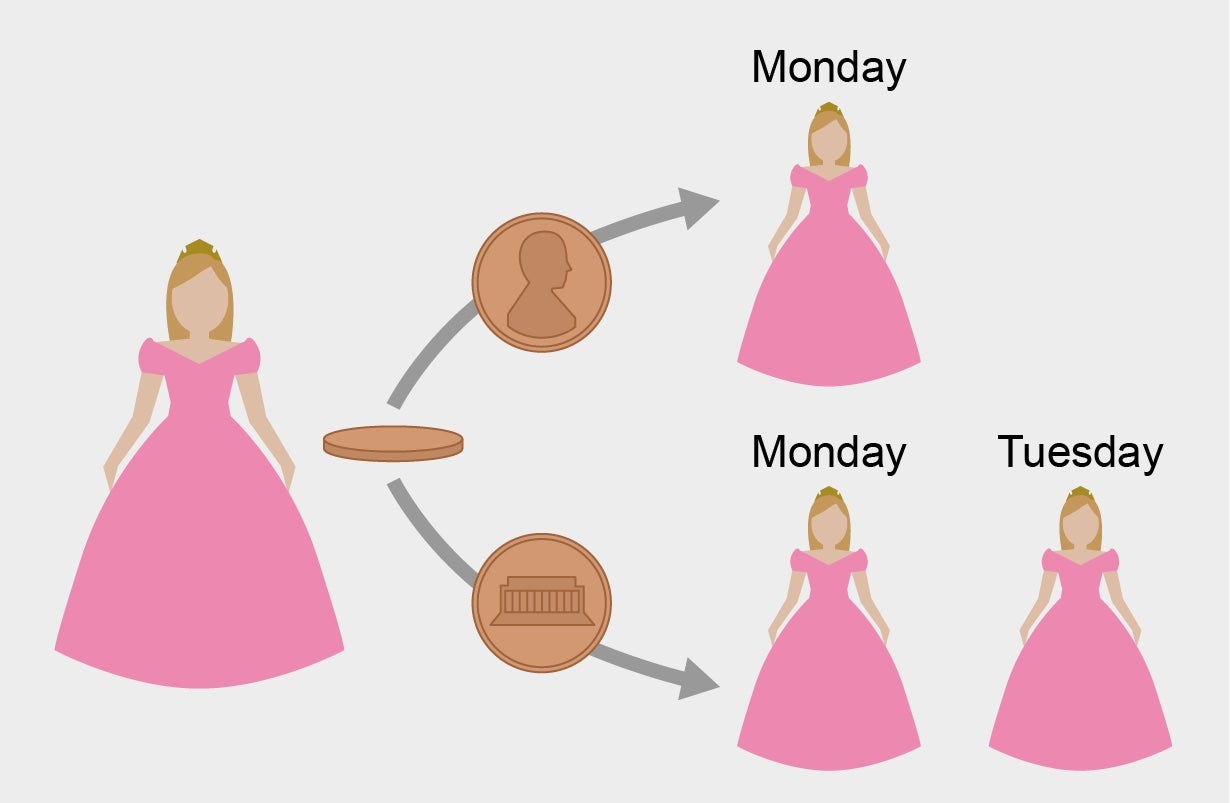
The trouble vexing the minds of industry experts is as follows: Sleeping Beauty agrees to take part in an experiment. On Sunday she is offered a sleeping capsule and falls asleep. A person of the experimenters then tosses a coin. If “heads” comes up, the scientists awaken Sleeping Beauty on Monday. Afterward, they administer a different sleeping capsule. If “tails” comes up, they wake Sleeping Magnificence up on Monday, place her back to rest and wake her up again on Tuesday. Then they give her an additional sleeping pill. In each instances, they wake her up all over again on Wednesday, and the experiment finishes.
[Read about the importance of thought experiments to Albert Einstein]
The crucial thing listed here is that simply because of the sleeping drug, Sleeping Magnificence has no memory of whether she was woken up right before. So when she wakes up, she cannot distinguish no matter whether it is Monday or Tuesday. The experimenters do not notify Sleeping Beauty both the consequence of the coin toss nor the day.
They request her just one query right after every time she awakens, nevertheless: What is the probability that the coin demonstrates heads?

Place by yourself in the placement of Sleeping Beauty: You wake up, you really don’t know what day it is, and you don’t know if you have been woken up right before. You only know the theoretical system of the experiment.
My initial instinct was that Sleeping Natural beauty should really guess ½.The probability of the coin landing on heads or tails—regardless of the rest of the experiment—is always 50 p.c. U.S. thinker David Lewis held the exact look at when he uncovered of the problem. After all, one could even flip the coin ahead of sending Sleeping Natural beauty to sleep. By the experiment’s style and design, she does not have any excess clues to the problem, so logically she must point out the chance as ½.
But there are also conclusive arguments in favor of a chance of ⅓. If you imagine by Sleeping Beauty’s practical experience, then a few eventualities can occur:
She wakes up Monday, and heads was thrown.

She wakes up Monday, and tails was thrown.

She wakes up Tuesday, and tails was thrown.
What are the chances for each individual celebration? You can examine this each mathematically and empirically. Suppose you flip a coin 100 instances and get tails 52 periods and heads 48 periods. Put a further way, the Monday/heads state of affairs takes place 48 situations, and Monday/tails and Tuesday/tails come about 52 instances just about every.
For the reason that Tuesday/tails often follows Monday/tails, the probabilities for all 3 events are equal—and have to thus be ⅓. When Sleeping Beauty is awakened and requested to solution what the probability of the coin toss was for heads, she really should consequently respond to ⅓, according to this reasoning.
 

Thinker of science Adam Elga of Princeton University, who popularized the Sleeping Beauty challenge in 2000, arrived to this summary. He formulated his argument in a mathematically audio way. If Sleeping Elegance is advised when she wakes up that today is Monday (M), then the probability of Monday/heads (M, H) and Monday/tails (M, Z) is indisputably equal: P(M, H) = P(M, Z) = ½, the place P stands for chance. On the other hand, if Sleeping Natural beauty wakes up and learns that tails have been thrown, then that day could similarly be either Monday or Tuesday (T), which means P(M, Z) = P(T, Z) = ½.
In accordance to the calculus of conditional possibilities, it follows that in the standard circumstance (with out Sleeping Attractiveness getting any more details), the three values are equivalent: P(M, Z) = P(M, H) = P(T, Z). Mainly because all 3 possibilities must insert up to 1, each and every particular person benefit is ⅓. In other phrases, mainly because Sleeping Beauty is awakened twice as typically in the scenario of tails as in the circumstance of heads, she ought to response with ⅓, from Elga’s point of look at.
Taking It to Extremes
How would you answer the dilemma now that you have read the two primary arguments? To get an even greater sense of the Sleeping Natural beauty problem, it can support to feel of a extra intense variation of the believed experiment.
Suppose that in the scenario of tails, Sleeping Magnificence will be awakened and questioned not just 1 additional time the subsequent day but a million situations (presumably at more compact intervals—because, even for a fairy tale character, this agenda would be brutal). If you wake her up and question her the chance that the coin landed on heads, the remedy ½ doesn’t appear rational in this situation. If the coin toss outcomes in tails, Sleeping Attractiveness is questioned a million instances in a row, and in the situation of heads, she is questioned just the moment.
But intense situations can also bolster the ½ camp’s place. For illustration, alternatively of a coin toss, a sports activities bet could be employed, these types of as a footrace pitting retired sprinter Usain Bolt versus singer Taylor Swift. In this circumstance, if Bolt, a world record holder in numerous functioning classes, defeats the pop star—as most folks would anticipate—Sleeping Attractiveness will only be woke up at the time on Monday. But if, contrary to all anticipations, Swift proves swifter, Sleeping Elegance have to wake up each and every working day for a thirty day period, 30 times in a row. The probability of Bolt losing to Swift is pretty minimal. But if we utilize the similar logic that determined the ⅓ reaction, we need to treat people situations with equivalent weight. Sleeping Attractiveness would still have to guess on a Swift victory after waking up mainly because in this—admittedly unlikely—situation, she could be awakened 30 times. Lewis uncovered this argument nonsensical. This assumed experiment, he as a result contended, supports the ½ faction.
Are you now fully baffled? You are not by itself. Has your impression changed? Mine has. I’m no more time fully certain by the ½ camp, at any price. I can also attain perception from the ⅓ placement.
This puzzle has some fascinating purposes. Philosophers and mathematicians can use it to think about determination-producing and chance broadly. For example, this imagined experiment illustrates how someone’s beliefs—in this situation, Sleeping Beauty’s—can lead to far more than 1 rational conclusion. It also underscores the difference concerning the quantity of experimental opportunities (this sort of as flipping heads as opposed to tails) and the attainable activities of somebody inside of an experiment.
This short article at first appeared in Spektrum der Wissenschaft and was reproduced with permission.
[ad_2]
Source hyperlink



